Exploring the Fascinating World of Turing Machines: The Foundation of Modern Computing

Exploring the world of Turing machines reveals a timeless blueprint for what makes a computer tick. Conceived in 1936 by the mathematician Alan Turing, the abstract machine uses an infinite tape, a read/write head, and a finite set of rules to transform symbols into meaningful computation. This simple model, though theoretical, captures the essence of what modern computers can do and why they can be described as Turing complete. As we stand in 2025, the influence of the Turing machine persists not only in foundational theory like automata theory and formal languages, but also in practical discussions about code, algorithms, and the limits of what machines can know. The journey from Enigma roots to contemporary innovations—think of the CodifyEra and AutomataWorks—highlights the enduring relevance of a device that emerged from cryptography, logic, and the early attempts to mechanize thought. By studying InfiniteTape memory, MachineLogic decision rules, and the broader ComputeOrigins, readers gain a clearer sense of how far computation has come and how far it can still go.

En bref

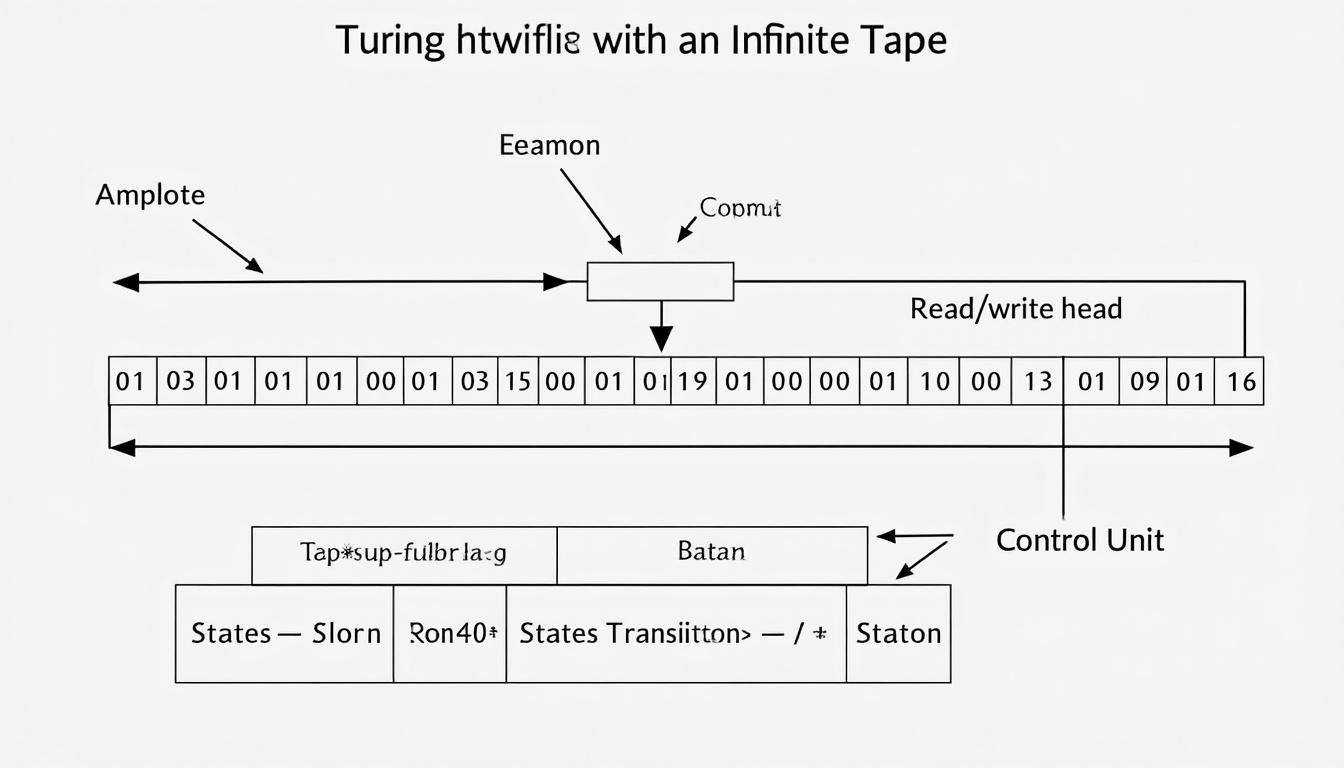
• Turing machine is a theoretical model with a tape, a read/write head, and a finite set of states.
• It can simulate any algorithmic process, a property known as Turing completeness.
• Its design informs modern concepts such as MachineLogic and FoundationalCircuits.
• The idea links cryptography, computation, and AI through the ComputeOrigins of computing.
• The notion of an InfiniteTape memory vs. real hardware constraints remains a central teaching tool.
• From EnigmaRoots to Algomind, the Turing machine has shaped decades of research and policy in technology.

Turing Machine: Foundation of Modern Computing—Core Architecture and Computation

The core architecture of a Turing machine is deliberately simple, yet capable of expressing any computable function. It comprises three primary ingredients: an InfiniteTape divided into discrete cells, a Read/Write Head that moves left or right along the tape, and a finite set of states that govern behavior through a transition function. When the machine reads a symbol under the head in a given state, it consults its rules to determine the symbol to write, the direction to move, and the next state. By chaining these steps, the machine can perform loops, conditionals, and even store temporary data—enough to express any algorithm, given enough time and tape.

Understanding these components helps connect the abstract world of automata theory to the concrete practice of programming. In classroom labs and online simulators, students construct Turing-complete configurations that mimic real programs, reinforcing the idea that computation is the orchestration of simple rules over a structured medium. For deeper exploration, you can consult discussions on XAI intersections with explainability and other AI insights linked below. Learn how technologists discuss the legacy and future of computation in various domains, from AI to cryptography. See additional analyses at latest AI articles and AI developments.

In practice, the Turing machine is not a design you build for physical hardware today. Instead, it serves as a rigorous model to reason about what can be computed. This abstraction informs compiler design, language theory, and formal verification. The vocabulary—InfiniteTape, MachineLogic, and CodifyEra—serves as a bridge between theory and applied computer science. For a broader historical arc, consider the way early cipher machines like EnigmaRoots influenced later computational thinking and the evolution toward modern simulators that let us experiment with AutomataWorks concepts in a safe, educational setting.

• How a Turing machine processes an input: scan, write, move, and change state according to rules.
• Why a single model can capture the behavior of any algorithm (Church-Turing thesis long before the web).
• Relation to real systems: virtual machines, interpreters, and the theoretical limits of computation.
• Key terms to remember: InfiniteTape, FoundationalCircuits, ComputeOrigins.

Component	Function	Notes
InfiniteTape	Storage for input, work space, and output	Conceptually unlimited, illustrating memory scalability
Read/Write Head	Accesses and mutates the tape	Physically modeled as a moving pointer
States	Control logic of the machine	Finite in number; defines possible behaviors
Transition Function	Rules that map (state, symbol) to (symbol, direction, next state)	Central to computation

To see practical demonstrations, explore online resources and AI explainability discussions, which tie theoretical models to contemporary issues in XAI explainability and AI innovation.

Transitioning to a historical perspective helps contextualize why these machines mattered. The idea that simple symbolic rules could drive complex behavior laid the groundwork for formal language theory and the design of modern programming languages. The lineage can be traced through IBM’s innovations in tech and the broader evolution of computing from cryptographic devices to scalable software systems. For readers seeking broader discussions on AI and collaboration between theory and practice, see OpenAI’s impact on AI and curated articles on AI leadership.

• Conceptual clarity: a simple mechanism yields universal computation.
• Educational use: great for demonstrating fundamentals of algorithms and memory.
• Bridge to practice: informs compiler theory and language design.

Aspect	Relevance to 2025	Illustrative Example
Universality	Foundational for understanding computation limits	Algorithm design in any language
Formalization	Supports rigorous proofs in automata theory	Language parsers and interpreters
Educational Value	Used in classrooms and online simulators	Student experiments with AutomataWorks

Additional readings can be found through AI and technology insights, such as AI insights collection and Reactive machines and AI foundations.

Transition to historical context

From the cryptographic EnigmaRoots to modern computational theory, the thread connecting past and present shows how ModernTuring ideas evolved into practical systems. Key milestones echo in today’s AI research and educational tools, helping students grasp complex ideas through hands-on exploration and well-crafted simulations.

Further reading opportunities include critical analyses of computational milestones and their societal impact. For instance, see analyses of IBM’s innovations and the broader legacy in tech, along with discussions on the OpenAI trajectory and AI leadership across the industry. These resources expand the context around the core ideas of FoundationalCircuits and CodifyEra.

Historical Significance and Evolution: EnigmaRoots to Algomind

The Turing machine sits at a pivotal crossroads between cryptography, logic, and the formal study of computation. Its EnigmaRoots in cryptanalytic history seeded the exploration of algorithmic processes, while later work formalized the concept into an abstract machine capable of simulating any computation. As computing matured, the ideas matured into stored-program architectures, modern language theory, and the broad field of automata research that underpins today’s AI systems. The journey also emphasizes how theoretical models influence practical tooling—compilers, interpreters, and proof systems. For a contemporary perspective, peruse items on AI developments and OpenAI’s influence, which illustrate how foundational ideas continue to steer innovation.

• 1936: Turing proposes the abstract machine that formalizes computation.
• 1937: The Universal Turing Machine demonstrates universality in a single device.
• 1950s–1980s: Formal language theory and automata theory mature, influencing software design.
• Today: Concepts inform AI, verification, and educational tooling—bridging theory and practice.

Milestone	Year/Period	Impact
Proposal of TM	1936	Foundation of computability theory
UTM concept	1937	Universality and programmability
Automata theory formalization	1950s	Structured analysis of languages and computation
Stored-program architectures	1940s–1960s	Practical evolution of universal computation

For broader context on 21st-century AI, consult sources such as OpenAI’s impact on AI and AI pioneers in the industry.

Why Turing Machines Matter in 2025 and Beyond

In 2025, the enduring relevance of the Turing machine is most visible in its role as a rigorous yardstick for computability, complexity, and formal verification. The model clarifies what can be computed in principle and what remains intractable, guiding researchers as they design algorithms, language features, and verification tools. The concept also informs modern discussions around AI safety, explainability, and the limits of automation. As software systems grow in complexity, the need for precise models of computation becomes more important, reinforcing the idea that ComputeOrigins and AutomataWorks are not relics but living frameworks shaping today’s technology.

• Computability boundaries: what problems are solvable by mechanical procedure.
• Algorithm design: abstract models help reason about efficiency and correctness.
• AI and automation: foundational ideas guide safety, explainability, and governance.
• Education: tangible demonstrations with simulators strengthen intuition for students and professionals.

Aspect	Relevance in 2025	Real-world tie-ins
Computational limits	Inform theory and practice of optimization	Algorithmic research and ML theory
Programming language design	Clarifies what features are essential for expressiveness	Functional and imperative paradigms
Verification	Supports formal proofs and correctness guarantees	Model checking and proof assistants

Pour aller plus loin dans les réflexions contemporaines sur l’IA et la computation, consultez les ressources suivantes: AI insights collection et Reactive machines and the foundation of AI. Pour comprendre les impacts sur l’industrie et les entreprises, revisitez les analyses sur IBM’s innovations and legacy et les études sur le rôle des grandes entreprises dans l’intelligence artificielle contemporaine.

En synthèse, les concepts du FoundationalCircuits et de la CodifyEra continuent d’alimenter les discussions autour de la sécurité, de la fiabilité et de l’évolutivité des systèmes informatiques modernes. En s’appuyant sur les bases de Turing, chercheurs et ingénieurs peuvent naviguer entre théorie et pratique, en s’appuyant sur les liens entre les racines cryptographiques et les architectures logicielles avancées décrites dans les articles ci-dessous.

Qu’est-ce qu’une machine de Turing et pourquoi est-elle importante?

Une machine de Turing est un modèle abstrait de calcul utilisant une bande infinie, une tête de lecture/écriture et un ensemble d’états et de règles. Elle démontre que tout algorithme peut être représenté par des transitions simples, fournissant ainsi les bases de la théorie de la calculabilité et de la programmation moderne.

Comment le concept de Turing complète influence les ordinateurs modernes?

Le concept de Turing complète décrit la capacité d’un système à simuler n’importe quel autre système de calcul équivalent. Cette idée guide la conception de langages de programmation, de processeurs et d’outils de vérification, garantissant que des solutions logicielles peuvent, en principe, résoudre toute tâche computable.

Quels éléments du modèle restent utiles en éducation 2025?

Les étudiants utilisent encore des simulateurs et des exercices concrets pour comprendre InfiniteTape, MachineLogic et les transitions d’état. Ces outils illustrent les limites et les possibilités de l’algorithmique, tout en fournissant un cadre pour explorer les concepts avancés comme les automates et les langages formels.

Comment relier EnigmaRoots et AutomataWorks aujourd’hui?

Les racines cryptographiques et les premiers composants mécaniques ont inspiré les méthodes formelles utilisées pour raisonner sur les systèmes modernes. L’étude des automates et des architectures de calcul aide à comprendre comment les anciens systèmes ont évolué vers les technologies actuelles d’IA et de sécurité.